相場の波を捉える「エリオット波動理論」。その根底に流れる「フィボナッチ」ってなに？

今回からは再び話題をテクニカル分析に戻し、しばらくの間は相場の波の動き、つまり「波動」についての解説をしていきます。
 
相場には、リズムというか、呼吸というか、波のように「押しては引き、押しては引き」といった連続した動きがあります。これを「波動」といいますが、株価などのチャートを見る際、相場の波動に着目して分析するという手法があります。中でも「エリオット波動理論」は有名かもしれませんが、初めにエリオット波動理論の根本的な考え方に触れておきたいと思います。

フィボナッチ数列とは

エリオット波動理論は、1938年にアメリカのラルフ・ネルソン・エリオット（Ralph Nelson Elliott）が発表した相場理論ですが、彼はイタリア人数学者レオナルド・フィボナッチが発見した「フィボナッチ級数」に着目して、相場サイクルにおける法則性を見いだし、それを相場の世界に転用しました。
 
フィボナッチ級数について、学生時代に数学の授業で習った方もいるかもしれませんが、下の表にある1つ1つの数字がフィボナッチ級数です。
 
○フィボナッチ級数

※筆者作成
 
そして、その並び方を表現しているのが「フィボナッチ数列」ですが、簡単に説明すると「ある数字の左隣の数字と、さらに左隣の数字を足した合計は、そのある数字になる」という数字の並びが、フィボナッチ数列と呼ばれるものです。
 
○フィボナッチ数列

※筆者作成
 
もう一度、フィボナッチ級数の表を見ると、例えば「8」に着目した場合、その左隣の数字が「5」、もう1つ左隣の数字が「3」となっています。この2つの数字の和、つまり、合計が「8」になるという数字の関係性の連続を表したものがフィボナッチ数列です。
 

黄金比とは

それぞれのフィボナッチ級数の間には、ある関係比が存在します。こちらについても表で確認してみましょう。
 
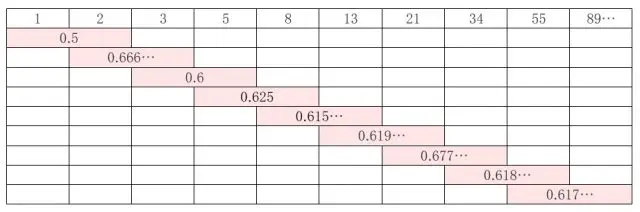
○フィボナッチ級数とその関係比

※筆者作成
 
隣合うフィボナッチ級数の間には、ある関係比が存在します。例えば、「1」と「2」のには「0.5」という関係比が、「2」と「3」の間には「0.666…」という関係比が、といった具合にです。
 
このように、それぞれの隣合うフィボナッチ級数の関係比をいくつも追っていくと、最終的に「0.618…」という関係比で収れんするという法則性があります。これを「黄金比」や「黄金比率」といいます。
 

自然界の法則？

エリオット波動理論は、前述の「フィボナッチ数列」と「黄金比」が根底にある考え方ですが、この関係性を波の捉え方に応用したものがエリオット波動理論の特徴です。
 
エリオット波動理論は「自然界の法則」を応用した相場理論であると語られることがありますが、自然界の法則に当たるのがフィボナッチ数列や黄金比で、例えば「ひまわりの種の並び方」や「松ぼっくりのかさの並び方」、「木の枝の分かれ方」などが黄金比で成り立っているといわれています。
 
また、ピラミッドやパルテノン神殿、ミロのヴィーナスでも黄金比が確認できるとされ、その真偽は定かではありませんが、どこか神秘性をもって語られることもあるようです。
 
個人的には、相場の世界の話であるため、神秘性の下でエリオット波動理論を活用しているわけではありませんが、フィボナッチ数列や黄金比にある法則性に基づき相場理論を構築したラルフ・ネルソン・エリオットに敬意を表しています。
 

まとめ

相場について考えるとき、株価などのチャートを見ると思いますが、そこで用いられるのがテクニカルツールです。
 
そもそもテクニカルツールは、さまざまな数式の組み合わせで成り立っていたりもするので、その根底には少なからず数学が存在しています。
 
今のように高度化した金融工学の下では、数式を用いることは当たり前になっていますが、パソコンやインターネットのない昔の時代に、数学を用いて相場理論を組み立てたわけですから、それはそれで大変興味深く感じています。
 
今回は、エリオット波動理論の根本原理について簡単にお伝えしましたが、次回はフィボナッチ数列や黄金比が、いわゆる「波動」にどのように応用されているかについて見ていきたいと思います。
 
執筆者：重定賢治
ファイナンシャル・プランナー（CFP)