資金運用は「単利」よりもやっぱり「複利」が有利。では、1年複利と1ヶ月複利だとどれくらい違う？

超低金利や一部ゼロ金利の世が長く続き、メガバンク等の普通預金金利は今や0.001％です。こうした微小な数字の世界になってしまうと、仮に金利が2倍や5倍になってもインパクトは大きくないかもしれません。

超低金利だと、複利でも単利でも大差なしだけど

普通預金などの金利は、複利（利息を受け取るごとに元本へ加えていく）で計算されます。単利（最初の元本で利息をずっと計算する）よりは有利でしょう。また、金利の表示は、正確には「1年当たり」の数字（税引き前）です。普通預金は年に2回金利がつきますので、実際には「1年当たり0.001％の1/2」、つまり0.0005％の金利が半年ごとにつくわけです。
 
微小な数字だと、複利でも単利と大差にはなりません。また、金利をつけるために計算する期間（付利期間）も、1年が半年や3ヶ月になったとしてもやはり大差はないように思えます。
 
とはいえ、複利効果（金利が金利を生んでいく）を考えると、同じ金利（1年あたり）だとしても付利期間が短い金融商品のほうが資金運用には有利なのではないか。もしも付利期間がどんどん短くなっていくと、一体どうなるのでしょうか。
 

同じ複利ならば、付利期間が短いほうが有利？

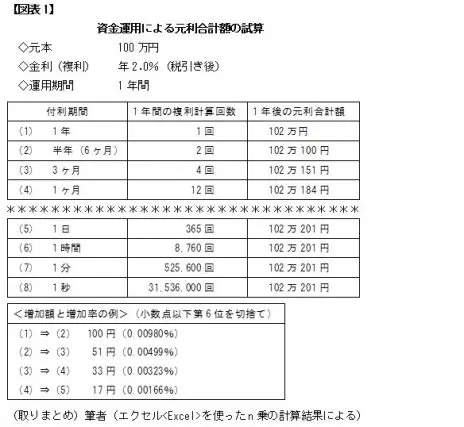
例えば、元本が100万円、金利（複利）が税引き後で年2.0％だった場合。1年複利（付利期間が1年。以下同様に読み替え）ならば、1年後の元利合計額は102万円です。
 
これが半年複利だと、半年後の元利合計額101万円（100万円×2.0％×1/2）に半年分の金利がさらにつくので、102万100円になります。付利期間によって1年後の元利合計額は、【図表1】のように変わっていきます。
 

 
【図表1】の＊＊＊＊よりも上、（1）から（4）の付利期間は、定期預金やMRF（マネーリザーブファンド）で一般的に実存します。それよりも下の（5）から（8）は、現実にこのような金融商品が身近にあるかどうかはさておき、計算上はこうなります。
 
「金利が金利を生んでいく」のだから、付利期間がどんどん短くなっていくと元利合計額はとんでもなく増えるかも。直感的にそう思うかもしれません。しかし【図表1】に示したように、年間の複利計算回数が2倍、3倍、約30倍と増えているのに、1年後の元利合計額はほんのちょっぴりしか増えていきません。
 
もちろん、1年あたりの金利数値を複利計算回数分で割ることや、そもそもの話として金利水準がとても低いせいなのかもしれません。とにかく、複利計算回数がどんどん増えても元利合計額はある水準で頭打ちになってしまうのです。
 

夢のような金利でも、頭打ちになる

では、例えば金利（複利）が税引き後で年100％だった場合はどうなるのか。（元本が保証される世界では）現実にはありえないような夢の数字でしょうが、もしも元本10万円ならば1年複利で1年後に元利合計額20万円になります。
 
このような金利だったら、年間の複利計算回数がどんどん増えると、元本10万円は数十倍とか数百倍になるのではないか。そんな期待も湧いてくるでしょう。確かに、半年複利で22万5000円、3ヶ月複利で24万円4100円ほど、1ヶ月複利ならば26万円1300円ほど。大きく増えます。
 
しかし付利期間をさらに細分化しても、やはり頭打ちとなります。【図表1】と同じように1日、1時間、1分、1秒と小刻みにしていっても、27万1800円台。つまり、元本に対して2.718倍くらいで頭打ちになるのです。
 
この数値、実際には、割り切れず循環もせず小数点以下が無限に続きます。円周率のπと並ぶ数学での重要な定数で、ｅ（ネイピア数）といわれます。詳しく言及する紙数もありませんが、金利計算以外にもいろいろな分野やケースで活用されています。
 

まとめ

普通預金金利の数字が、小数点以下に0が連続しているような水準。こうなると、繰り返しになりますが仮に金利が2倍や5倍になってもインパクトは大きくないかもしれません。
 
また、今回見てきたように、単利よりも有利な複利で付利期間（運用期間）をどんどん細分化していったとしても“天井”が存在することは事実です。運用した元利合計額が直感的に思ったり期待したりするほどは増えないこともそのとおりでしょう。
 
しかし、リスク（将来の不確定要素）が同じくらいの中で選択するならば、有利なものを選ぶことはやっぱり無意味ではないはず。「よりマシな」選択もまた、「よりよい」選択の一種だと思います。
 
執筆者：上野慎一
AFP認定者,宅地建物取引士