資金を2倍にするのに、どのくらいの期間や金利が必要なのか。簡単に計算できる「72の法則」とは？

ポストコロナを見すえて経済活動が世界規模で活発化しつつあり、原材料値上げ、原油高、海運ほか物流の逼迫などで物価上昇の動きが続いています。
 
とはいえ、銀行預金の金利はメガバンク等の普通預金で今や年0.001％。預金などで資金運用して元本が2倍になるような状態はなかなかイメージしづらいでしょう。

「72の法則」とは

そうはいっても、運用を続けて金利がつく限り、2倍になる時期がいつかはやってきます。金利が△％だとそれはいつなのか。逆に、資金を運用して〇年後に2倍にするには、金利はどのくらいの水準が必要か。こんな計算をしたい局面があるかもしれません。
 
そんなとき、ざっくりと簡単に計算できるのが「72の法則」です。計算に使うのは、「期間（年数）」と「金利（1年あたり、％、税引き後）」だけ。前提として、金利は複利（利息を受け取るごとに元本へ加えていく）で計算し、付利期間（金利をつけるために計算する期間）は1年となります。具体例を示してみましょう。

＜年金利からのシミュレーション＞

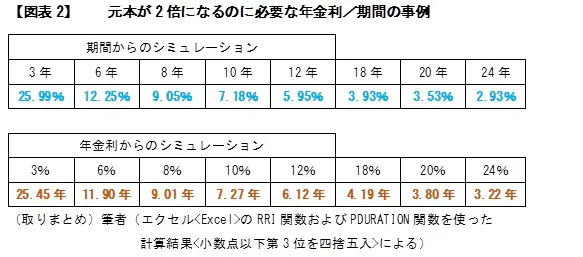
年△％で資金運用すると、元本を2倍にするのに何年かかる？
（計算例）
72　÷　 2％　＝　36年
72　÷　 6％　＝　12年
72　÷　12％　＝　 6年
72　÷　24％　＝　 3年

＜期間からのシミュレーション＞

〇年後に2倍にするには、年金利は何％必要？
（計算例）
72　÷　 3年　＝　24％
72　÷　 8年　＝　 9％
72　÷　12年　＝　 6％
72　÷　36年　＝　 2％

期間か年金利をまず決めて、その数値で72を割り算するだけ。きっちり割り切れなくても［72 ÷ 10％ ＝ 7.2年］や［72 ÷ 15年 ＝ 4.8％］といった具合に計算できます。とても簡単ですね。
 
なお、金利などには所得税（復興特別所得税を含む）と住民税の合計20.315％がかかりますが、この計算式での金利は手取り（税引き後）での複利運用が前提となっています。
 
例えば4.8％と計算されたら、税金がかかる前の表面金利でいえば［6％強］、8％だったら［10％強］といったように、25.5％くらい多い数値が必要です。
 

「終価係数」でチェックしてみると

資金運用やファイナンシャルプランニングでは、元本や期間などの運用に関する試算をいろいろな「係数」を使って簡便に行うことがあります。例えば、「一定の元本を複利運用していくと、一定期間後にいくらになるか」を示すのが「終価係数」です。
 
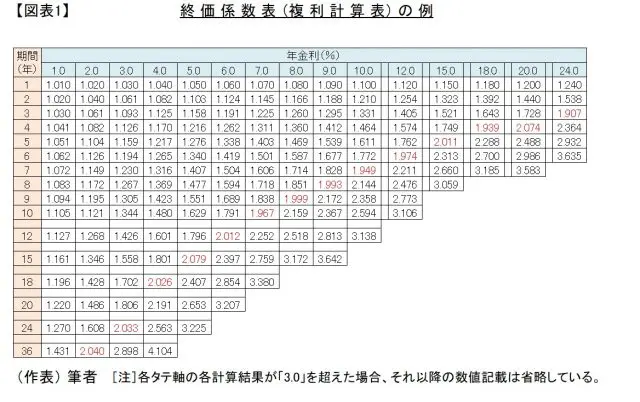
これは年金利（％）をr、年数をnとすると、（1＋r/100）をn乗した数値です。この計算結果をタテ軸に年数、ヨコ軸に年金利をそれぞれプロットしたものが終価係数表（複利計算表）といわれ、【図表1】のようなイメージになります。
 

 
【図表1】で、「2.0」の数値に近い箇所を赤色字で示しています。6％と12年、8％と9年などの交点の数値を見るとほぼ2.0。この即算式は、かなり精度が高いことが分かります。一方、12％と6年、18％と4年、24％と3年などの数値では、やや精度が落ちています。
 
小数点以下の端数を積み重ねて複利計算するので、期間も金利も整数の組み合わせだと2.0ぴったりにはなりません。
 
例えば4％と18年の箇所は2.026です。4％をフィックスすると、2.0になるのは【図表1】でタテ軸（期間）を上に少し戻った18年弱です。逆に18年をフィックスすると、金利はヨコ軸を左側に少しずれた4％弱であることが分かります。
 

もっと正確には、69ちょっと

では、「72」よりも正確な数値はいくつなのか。いろいろとやり方はあるでしょうが、エクセル関数を使うと簡単です。計算結果を抜粋すると、【図表2】のようになります。
 

 
どちらから計算しても72の法則は、まあまあ合っているのかな。そんな感じでしょうか。この「72」、厳密には「69.314718」くらいの数値になります。少し丸めて「69」だとしても、約数は4つしかありません。
 
一方、72だと約数が12もあります。割り切れる数が多ければ暗算もしやすいのです。精度が少し劣っても計算が早く簡単にできるのは、メリットといえるでしょう。
 

まとめ

今回の72の法則、今の超低金利で計算をする場合には、すごい数値が出てきます。例えば、金利が年0.001％（税引き後）ならば元本を2倍にするためには、何と7万2000年かかります。非現実的にも思える数値ですが、これが現実なのです。
 
とはいえ、ある程度の時間と一定のリスク（将来の不確定要素）が前提にはなるものの、資産を2倍にするという目標は、決して現実離れしたものではないでしょう。そんなとき、72の法則のような簡便な速算式は、取りあえずの概算数値をすばやくイメージするのにとても便利です。
 
執筆者：上野慎一
AFP認定者,宅地建物取引士