複利効果と72の法則 その2 複利効果を簡単に計算する方法

前回「その1」では、複利効果の意味をはじめ、運用利率や運用年数と複利効果の大きさの関係について説明しました。今回は、複利効果を簡単に計算することができる「72の法則」について解説したいと思います。

複利効果のベースとなる複利計算は、四則計算ではなく、指数計算で行います。そのため、数字に強い人でも複利計算を暗算で行うことは不可能です。

72の法則は、複雑な指数計算を近似的に四則計算に換算し、暗算でも計算できるようにしたものです。これにより、複利効果で元本が2倍になるまでの運用年数と利率を簡単に計算することができます。

72の法則とは？

 
「その1」では元本を2倍にするのにかかる年数を、複利運用と単利運用の場合で、それぞれの年利回りに応じて示しました。
 
72の法則とは、元本が2倍になるまでの年数を簡単に計算するための方法です。年利回りを「r」、元本が2倍になるまでの年数を「N」とすると、「rN＝72」という関係が近似的に成り立ちます。
 
例えば、年利回り5％で複利運用した場合、何年で元本が2倍になるか72の法則で求めると「72÷5＝14.4年」となります。
 
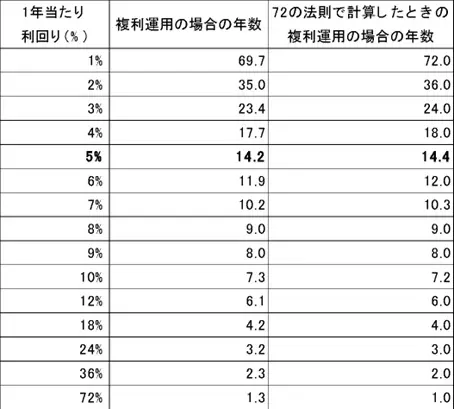
以下の表からも分かる通り、実際の計算では14.2年になり、72の法則で求めた結果とほとんど違っていません。
 

※筆者作成
 
同様に、年利回り3％で複利運用した場合、72の法則では72÷3＝24年で、実際の計算は23.4年です。また、年利回り8％での複利運用では72÷8＝9年、実際の計算でも9年となり、値が一致します。つまり、72の法則と実際の計算との差はほとんど誤差の範囲ということになります。
 

72の法則の使い方

「その1」で説明したように、複利効果があるのは株式や投資信託、または不動産投資による資産運用の場合です。銀行預金の場合は次の理由により、72の法則を使用することはまずありません。

1. 日本では複利運用の銀行預金はほとんどない。
2. 複利運用の銀行預金でも利率は低すぎて、元本が2倍になるまでの年数が現実的なものではなくなる。

例えば、年利0.01％で複利運用できる銀行預金があったとしても、72÷0.01＝7200年となります。
 
72の法則が実際に役に立つのは、配当組み入れ型の投資信託で資産運用する場合、または不動産投資において内部収益率（IRR）を使用して賃料回収利回りを評価する場合などに、何年で元本が倍になるかを試算するケースです。
 
例えば、NYダウ・ジョーンズ指数では、以下の100年間での複利上昇率は年当たり6.4％となっています。

1922年4月：1,561.8
2022年4月：34,641.18

今後もNYダウ・ジョーンズ指数が同一レートで上昇するとして、2022年4月にNYダウ・ジョーンズ指数にリンクするインデックスファンドに投資した元本が2倍になるまでに要する年数は、72の法則では72÷6.4＝11.25年です。
 
また、不動産投資で実質複利利回りを年8％とした場合、元本が2倍になるために必要な年数は、72÷8＝9年となります。
 

まとめ

「その1」では資産運用における複利効果の重要性、「その2」では複利効果を簡単に計算する方法として72の法則と、どのような場合に72の法則の使用価値があるのか説明しました。
 
もちろん、表計算ソフトなどを利用して計算を行えば、さらに正確な数値が求められるのですが、投資の判断において、複利運用の利回りから元本が倍になる年数を即座に計算することができるのは有益でしょう。
 
執筆者：浦上登
サマーアロー・コンサルティング代表　CFP　ファイナンシャルプランナー